
Because of these different definitions, the two q values cannot be usefully compared. For the Dunnett test, q is the difference between the two means (D) divided by the standard error of that difference (computed from all the data): q=D/SED.
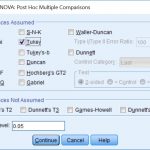
By historical tradition, this q ratio is computed differently for the two tests. Prism reports the q ratio for each comparison.If you choose 95% intervals, then you can be 95% confident that all of the intervals contain the true population value. This confidence interval accounts for multiple comparisons. Both tests can compute a confidence interval for the difference between the two means.It is possible to compute multiplicity adjusted P values for these tests.These decisions take into account multiple comparisons. The results are a set of decisions: "statistically significant" or "not statistically significant".This gives the test more power to detect differences, and only makes sense when you accept the assumption that all the data are sampled from populations with the same standard deviation, even if the means are different. When you compare mean A to mean C, the test compares the difference between means to the amount of scatter, quantified using information from all the groups, not just groups A and C. This gives you a more precise value for scatter (Mean Square of Residuals) which is reflected in more degrees of freedom. Both tests take into account the scatter of all the groups.The Dunnett test compares every mean to a control mean.Prism actually computes the Tukey-Kramer test, which allows for the possibility of unequal sample sizes. The Tukey test compares every mean with every other mean.

They cannot be used to analyze a stack of P values.

Choose to assume a Gaussian distribution and to use a multiple comparison test that also reports confidence intervals. Prism can perform either Tukey or Dunnett tests as part of one- and two-way ANOVA.


 0 kommentar(er)
0 kommentar(er)
